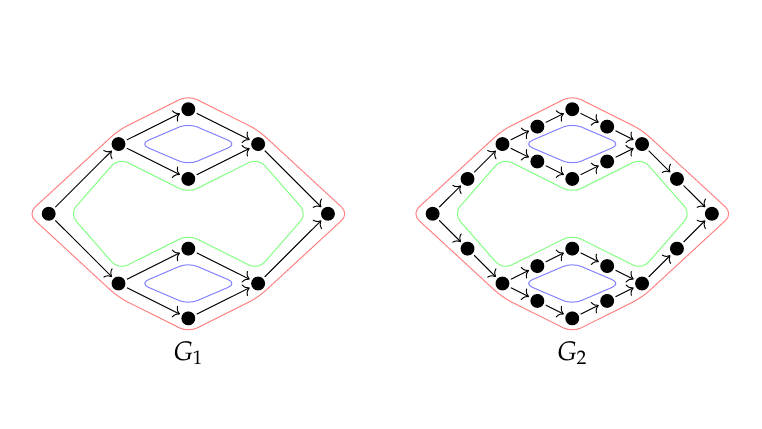
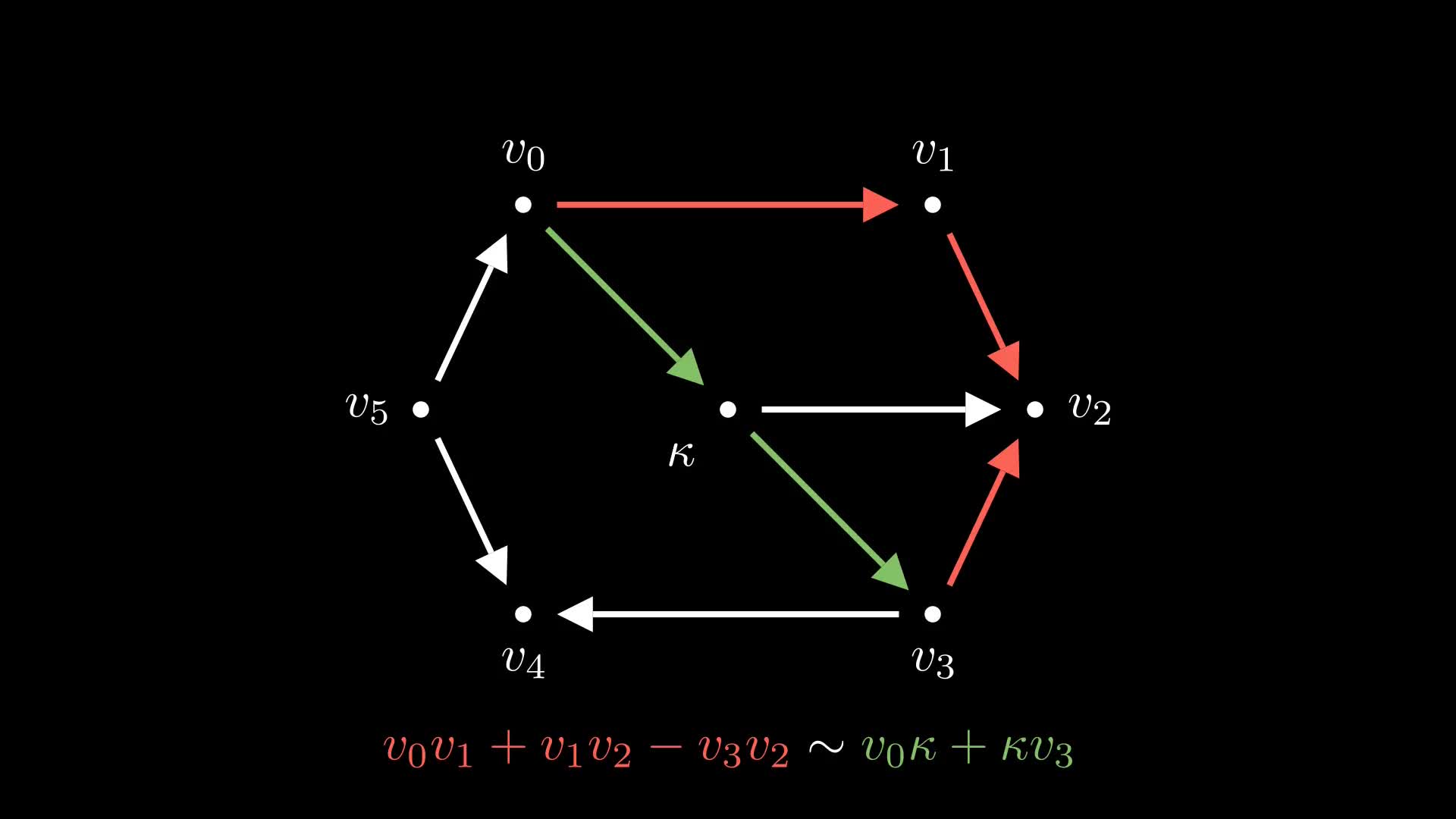
Weighted di­graphs are used to model a va­ri­ety of nat­ural sys­tems and can ex­hibit in­ter­est­ing struc­ture across a range of scales. In or­der to un­der­stand and com­pare these sys­tems, we re­quire sta­ble, in­ter­pretable, mul­ti­scale de­scrip­tors. To this end, we pro­pose grounded per­sis­tent path ho­mol­ogy (GRPPH) - a new, func­to­r­ial, topo­log­i­cal de­scrip­tor that de­scribes the struc­ture of an edge-weighted di­graph via a per­sis­tence bar­code. Joint work with Heather A. Harrington and Ulrike Tillmann.

Path ho­mol­ogy is a topo­log­i­cal in­vari­ant for di­rected graphs, which is sen­si­tive to their asym­me­try and can dis­cern be­tween di­graphs which are in­dis­tin­guish­able to the di­rected flag com­plex. In Erdös-Rényi di­rected ran­dom graphs, the first Betti num­ber un­der­goes two dis­tinct tran­si­tions, ap­pear­ing at a low-den­sity bound­ary and van­ish­ing again at a high-den­sity bound­ary. In this video, I briefly de­scribe tech­niques for study­ing these tran­si­tions, with more de­tails on the arXiv pre-print.